TDOA (Time Difference Of Arrival), also known as multilateration, is a well-established technique for the geolocation of RF emitters. Using three or more receivers, TDOA algorithms locate a signal source from the different arrival times at the receivers. We trust that existing users of CRFS’s TDOA geolocation know, from their own experience, that it is very accurate and effective for most signal types.
New users often ask us, “How accurate is TDOA?”. Unfortunately, a short and simple answer is not necessarily the best one. We’ll give you the short answer and a longer answer below.
The Short Answer
TDOA geolocation results can give locations with as little as ten meters of uncertainty. Unlike other geolocation techniques, TDOA can provide accurate geolocation even for signals with power levels below the noise floor.
That’s the short answer, but if you feel like an answer that includes “as little as” isn’t really an answer at all, then please keep reading.
The Slightly Longer Answer
We say “as little as” because there are a number of factors that put limits on the accuracy of TDOA. The overall geolocation accuracy can be no better than the worst of these limits. Our discussion will apply to any receiver technology, although we’ll illustrate it with graphics produced by CRFS software, and sometimes we’ll mention the ways that CRFS systems mitigate the effects of some sources of inaccuracy.
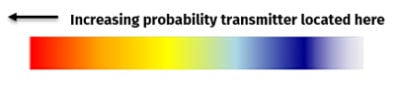
When we show probability heat maps for the location of a transmitter, the scale goes from violet to red with increasing probability:
Factor 1: Timing Accuracy
Precise synchronization between receivers is essential for achieving high-accuracy TDOA. In remote, distributed-receiver networks, timing is usually sourced from GPS (or another positioning network such as GLONASS or BeiDou). TDOA accuracy is strongly dependent on the quality of reception: very good GPS conditions allow the synchronisation error between receivers to be less than 30 ns RMS, which corresponds to an accuracy of
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 = 𝑠𝑝𝑒𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡×𝑡𝑖𝑚𝑒=3×108𝑚/𝑠×30 𝑛𝑠=9 𝑚
but under typical conditions accuracy will often be limited to a few tens of meters.
If we need TDOA geolocation when GPS is unavailable (for example, because of jamming or solar flares), an alternative synchronization method is necessary. During a temporary outage, receivers can base their timing on the GPS signal that was received before reception was lost; CRFS offers a GPS holdover module to enable this. The accuracy of the timing and geolocation will gradually deteriorate over the minutes and hours after loss of the GPS signal. Alternatively, a direct synchronization link between receivers eliminates the need for GPS reception altogether, and may also allow more precise synchronisation than GPS. This is the role of CRFS’s optical SyncLinc timing system, which can provide precision below 25 ns independently of GPS conditions.
| Advantages | Disadvantages | |
|---|---|---|
|
GPS
|
|
|
|
GPS Holdover
|
|
|
|
RFeye SyncLinc
|
|
|
Factor 2: Sample Rate and Bandwidth
The time resolution, and consequently the spatial resolution, you can expect from your TDOA network will depend on the sample rate. For example, sampling a signal at 10 MHz gives a time resolution of
𝑡𝑖𝑚𝑒 = 1𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦=110 𝑀𝐻𝑧=0.1 µ𝑠
which corresponds to a spatial resolution of
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 = 𝑠𝑝𝑒𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡×𝑡𝑖𝑚𝑒=3×108𝑚/𝑠×0.1 µ𝑠=30 𝑚<
Unfortunately, it’s not just a matter of increasing the sample rate to improve TDOA accuracy. If we increase the sample rate much beyond the modulation rate or bandwidth of the signal, we get a law of diminishing returns, as the variations between successive data samples are increasingly related to noise rather than to variations in the signal. The optimal sample rate for TDOA will be comparable with the bandwidth of the signal being geolocated, and the accuracy will be given approximately by
𝑎𝑐𝑐𝑢𝑟𝑎𝑐𝑦 = 𝑠𝑝𝑒𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡4×𝑏𝑎𝑛𝑑𝑤𝑖𝑑𝑡ℎ = 3×108𝑚/𝑠4×𝑏𝑎𝑛𝑑𝑤𝑖𝑑𝑡ℎ
which is consistent with an accuracy of 10 m at bandwidth 10 MHz, worsening to 100 m at 1 MHz, and 1 km for a bandwidth of 100 kHz.
The graph below shows how the uncertainty in position decreases as we increase the sample rate, for PSK signals with modulation rates of 8 MHz and 30 MHz.
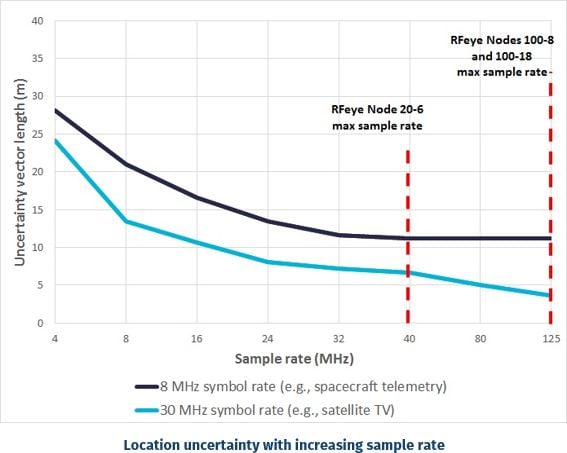
We can see from the graph that, to achieve the best possible geolocation performance for wideband signals, we need a receiver with a high maximum sample rate (for example, the RFeye Node 100-8 or 100-18 rather than 20-6).
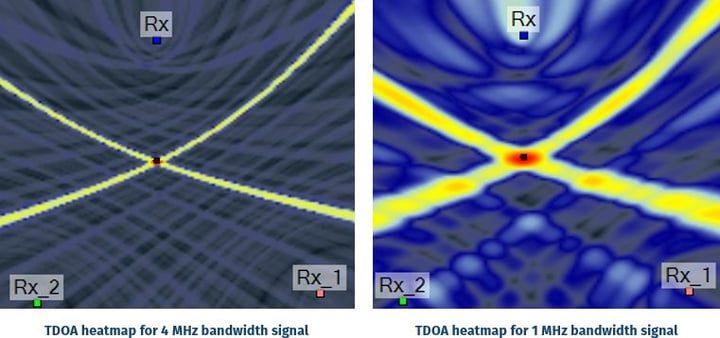
A time difference in TDOA is calculated from the position of a peak in the cross-correlation function of two receivers, so the time resolution can be related to the width of the correlation peak. The narrower the bandwidth of a signal, the wider that peak will be. The correlation peaks for a 4 MHz bandwidth signal and an equivalent 1 MHz bandwidth signal are plotted below.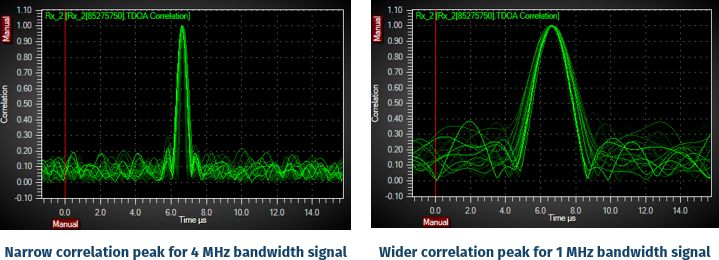
The wider correlation peak corresponds to a greater uncertainty in the time delay, and hence in the location, as shown by the heat maps below. The receivers are located approximately at the corners of an equilateral triangle of side length 9 km.
Factor 3: Signal Periodicity
If a signal is periodic, the cross-correlation function will have more than one peak, corresponding to more than one possible value for the time delay (and therefore the location). If more than one location is feasible (which is more likely if the period is short), there will be uncertainty in the geolocation. This is best illustrated with a graphic; the curves of different colours represent the same periodic signal at different receivers:
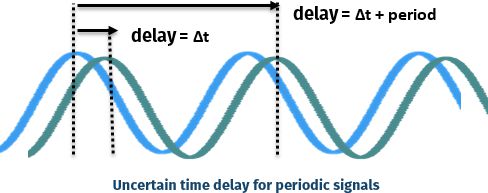
The distance between possible locations will be of the order
3×108×𝑝𝑒𝑟𝑖𝑜𝑑
so TDOA is likely to be successful if the period is milliseconds or greater (possible locations are hundreds of kilometers apart), and unlikely to be successful if the period is microseconds or less (locations are no more than hundreds of meters apart). The worst case is a CW (unmodulated continuous wave) signal, for which TDOA geolocation is unlikely to be useful, except for frequencies below 1 MHz.
For periodic signals (as also for narrowband signals), AOA geolocation performs much better than TDOA. This is why CRFS recommends a hybrid system combining AOA and TDOA techniques, so that geolocation performance is optimized across all signal types and scenarios. The contrasting advantages and disadvantages of different geolocation techniques are explored in other CRFS publicationsi.
Factor 4: Network Geometry
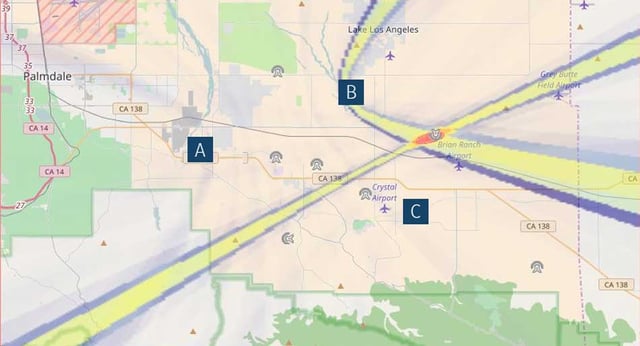
TDOA accuracy is affected by the transmitter location relative to the receiver network, and also by the geometry of the network, because of an effect called ‘dilution of precision’. The geolocation will be most accurate at a location where a small change in time difference results from a small change in location, and less accurate if a larger change in location is needed to produce the same small change in time difference.
To a first approximation, the best accuracy will be achieved when the transmitter lies within the envelope of the three (or more) receiver locations. Outside this envelope, inaccuracies introduced by other factors will be magnified by the geometry. The two images below show location probability heat maps for transmitters within, and outside, the envelopes. The larger, red area for the latter transmitter indicates a greater uncertainty in location. As before, the receivers are near the corners of an equilateral triangle with sides 9 km long.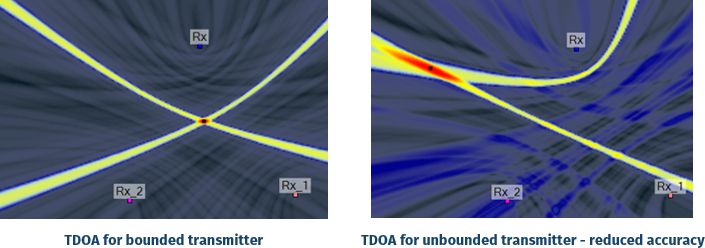
Factor 5: Obstacles
As with any monitoring or geolocation task, the receivers need to be able to “see” the signal: obstacle shadowing will prevent successful TDOA geolocation. Multipath effects from reflected and diffracted signals can also complicate geolocation, although TDOA is relatively robust against multipath in comparison with AOA geolocation techniques. The biggest obstacle of all, the earth’s curvature, can also limit TDOA over long ranges.
The presence of obstacles is an important factor for network optimisation. The greater the receiver heights, the easier it will be to see around obstacles such as mountains, buildings and the earth itself. For any given height above ground level, optimum positioning can also improve geolocation performance, e.g., by placing receivers on the tops of hills rather than behind them.
It is often helpful to use simulation and modeling tools, such as those offered by CRFS, to model these obstacle and receiver positioning effects as well as the other factors affecting TDOA accuracy that we have discussed. This allows geolocation scenarios to be tested and receiver placement to be optimized before a real-world network is implemented.
In Conclusion
Hopefully this has helped explain why we don’t like to give the short answer to the question, “How accurate is TDOA?” In analyzing any TDOA system, we need to remember all the factors discussed in the longer answer, and the accuracy we can achieve will inevitably depend on the details of the system. We can’t use a single “headline figure” for TDOA accuracy, and, if a single figure is quoted, it’s unlikely to be valid.
If you have a scenario in mind and want to know what kind of TDOA accuracy you can expect, then get in touch – we can even show you a live demo!
If you want to learn more about TDOA geolocation in general, check out our recent webinar TDOA – A modern geolocation solution.

White paper
Passive geolocation with 3D TDOA
This white paper addresses the basic operating principles of 3D TDoA; Practical limitations on its accuracy; Applications of the technique.



